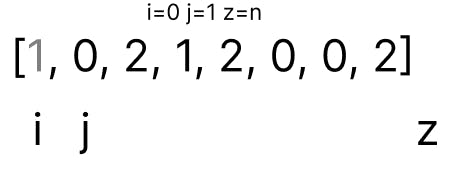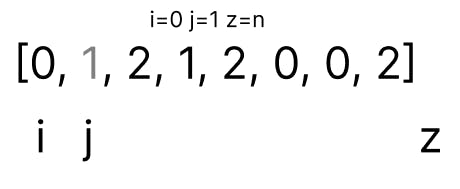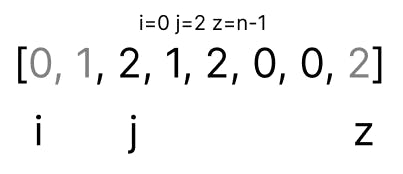Sorting Array of 0s, 1s and 2s

Sorting an array is a tedious task and usually takes nlogn time. But since we know that the array contains only 0s, 1s and 2s. We can do this sorting in logn time.

Simple Approach

One simple approach would be to find the frequency of each element(i.e. 0s, 1s and 2s) and create an array with this information.

Here is how we can do this with JavaScript methods:

function simple_sort_0_1_2(arr) {
  let freq = arr.reduce((acc, curr) => {
    if (!!acc[curr]) {
      acc[curr] += 1;
    } else {
      acc[curr] = 1;
    }
  }, {});

pointer_sort_0_1_2([1, 0, 2, 1, 2, 0, 0, 2])
-> [0, 0, 0, 1, 1, 2, 2, 2]

This approach requires us to create a new array and a frequency map for our array. We can do better than that when it comes to space complexity.

Three Pointer Approach

I would recommend you try and sort an array of 0s and 1s with two pointer method before trying out this problem as it is an extension of that problem.

To begin building our logic, let's see a sorted array of 0s, 1s and 2s.

Let's put three pointers that mark either beginning or end of the three sections.

i is at the end of 0s
j is at the end of 1s
and k marks the start of 2s

Initially, our array would be unsorted. So let's do that.

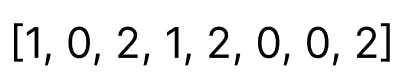
Now that we have our initial array, we need to think of some initial values for our pointers i, j and k.

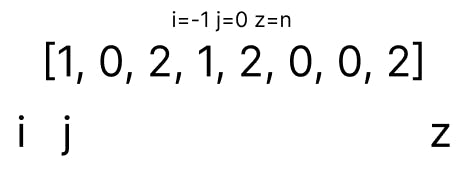
i is kept just outside of the array at -1
j is at the first element 0
and z is at n just outside the end of the array.

This is the initial arrangement that I prefer. You will see why we put i and z out of the array once we look at the logic.

Now we will discuss how to proceed as we encounter each of the three kinds of elements. Also, note that we will iterate over the array until j < z is true and j is the pointer we will be monitoring.

As we can see in the diagram above, arr[j] is pointing to 1. When arr[j] is equal to 1, we simply move to the next element by doing j++.

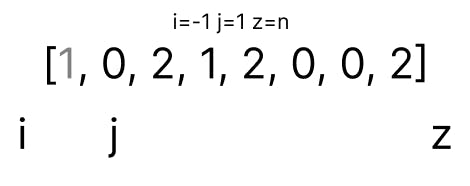
Notice that right now j is pointing to the end of known 1s.

The next element is 0. When arr[j] points to 0, we increment i by one and swap the elements at arr[i] and arr[j]. At last, we move j to the next element.

You are doing great! Just stay with me for a little longer. Because now we have come across a 2. In this case, we decrement the z by one and swap arr[j] and arr[z]

Notice that we haven't moved j this time. This is because we haven't checked the value that we swapped with arr[z]. In the next iteration, we would have again arr[j] = 2 and we would again follow the steps we just discussed.

By repeating these steps until j < z we will end up with something like this:

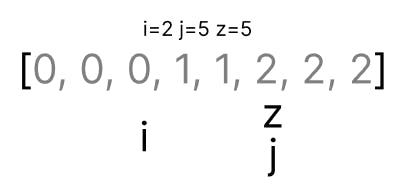
The pointers are a little off than what I imagined tbh. But that is fine. Pointers can be a little off at times and you might have to make slight adjustments in your code as well. Just know that it is part of your journey. I won't be making changes to this one because we were able to get the desired output. Let's look at the code now.

function pointer_sort_0_1_2(arr) {
  let res = arr;
  let l = -1;
  let r = res.length;
  let m = 0;
  while (m < r) {
    if (res[m] === 0) {
      l++;
      [res[m], res[l]] = [res[l], res[m]];
      m++;
    } else if (res[m] === 1) {
      m++;
    } else {
      r--;
      [res[m], res[r]] = [res[r], res[m]];
    }
  }
  return res;
}

pointer_sort_0_1_2([1, 0, 2, 1, 2, 0, 0, 2])
-> [0, 0, 0, 1, 1, 2, 2, 2]

After going through all that explanation. It is easy to understand this code. Do dry run the code with pen and paper when you get time.

This problem was more difficult than the ones we have done in the past but don't worry you will get used to this feeling. Next, we will sort an array of negative and positive integers.

Sorting Array of 0s, 1s and 2s

Table of contents

Simple Approach

Three Pointer Approach