Introduction
Matrix is defined as a group of similar or different data values arranged in rows and columns. In programming, matrices are represented as two-dimensional arrays. They are easily one of the most heavily used data structures in the field of computer graphics and can also be used to implement network graphs.
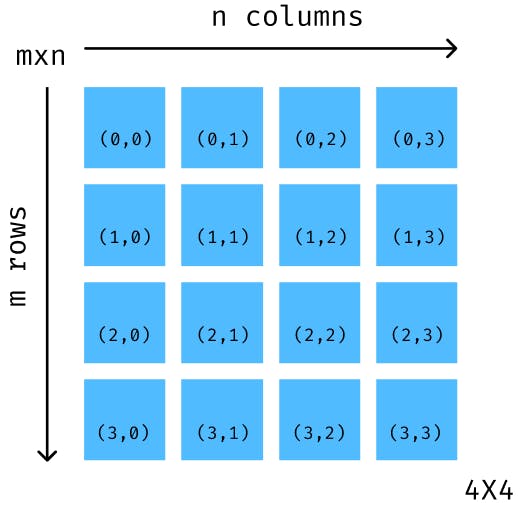
A matrix can represent different sorts of data based on different scenarios and it is through this versatile use of matrices that the need for various matrix traversal methods arises. In this article, we will check out the following traversal methods:
- Row-wise Traversal
- Column-wise Traversal
- Breadth First Search Traversal
- Depth First Seach Traversal
Row-wise Traversal
In row-wise traversal, we traverse through the matrix starting from the first row, moving left to right, all the way to the last row. It is a common way to travel a matrix.

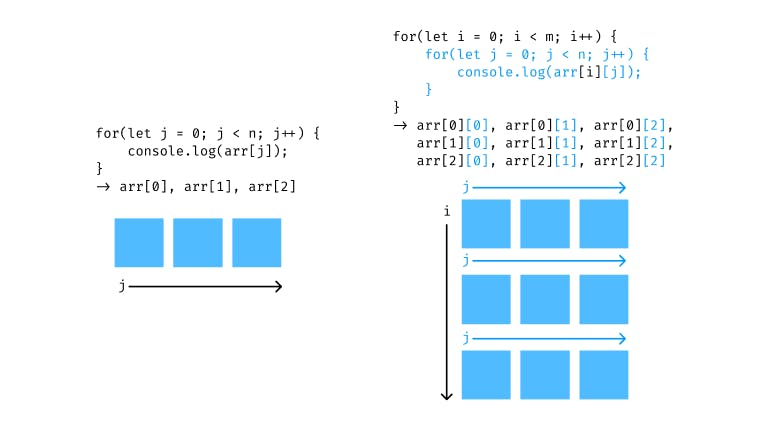
For row-wise traversal of an mxn matrix, all we need to do is to traverse m rows, each containing n elements.
In the following code we iterate over an array of n elements:
for (let j = 0; j < n; j++) {
console.log(arr[j]);
}
// arr[0], arr[1], arr[2], ... , arr[n]
Now we iterate over this code m number of times:
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
console.log(arr[i][j]);
}
}
// arr[0][0], arr[0][1], ... arr[0][n],
// arr[1][0], arr[1][1], ... arr[1][n],
// .
// .
// arr[m][0], arr[m][1], ... arr[m][n]
Here is a visual representation of above-mentioned code snippets:
Column-wise Traversal
In column-wise traversal, we iterate over the matrix starting from the first column, moving top to bottom, up to the nth column.

Before we iterate an mxn matrix, let's observe values of first and second index of a single column:
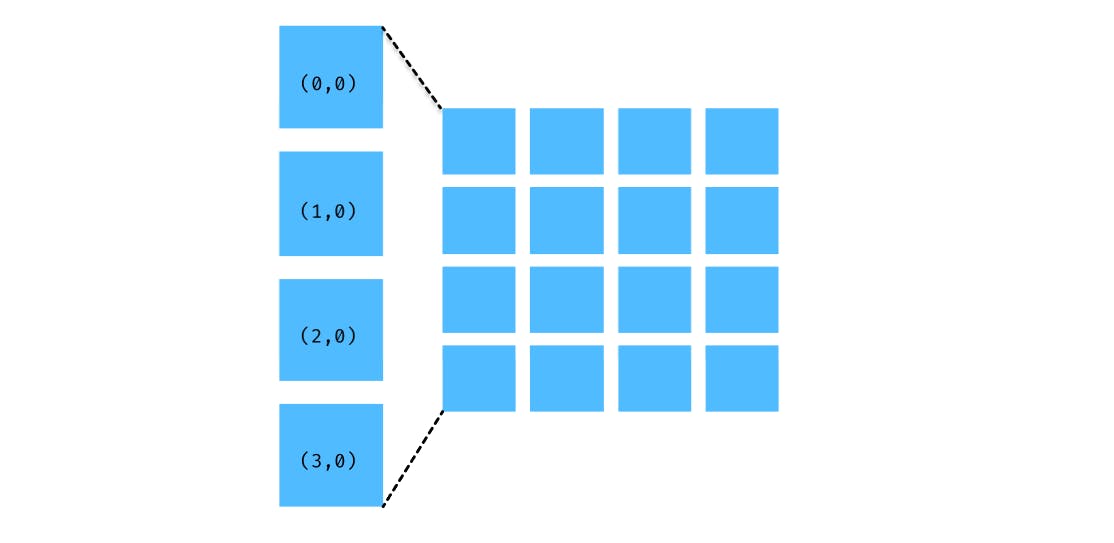
We can traverse the above column using the following code:
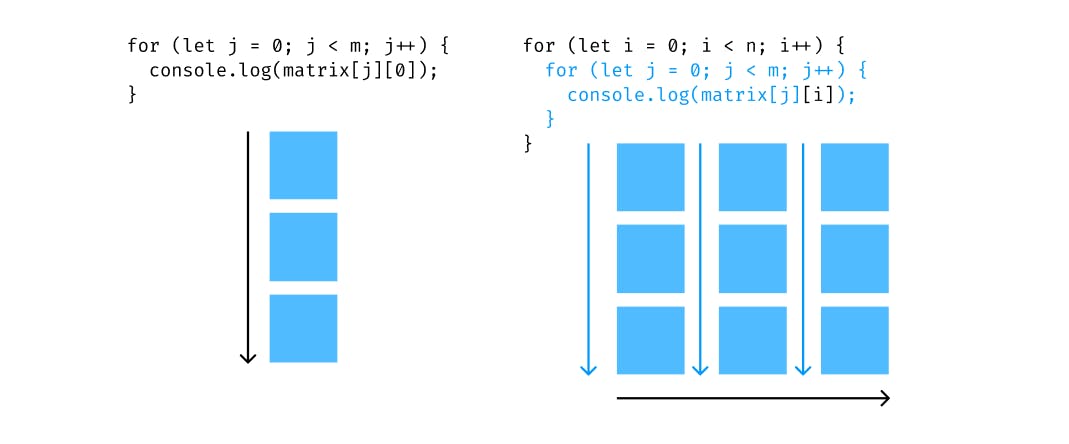
for (let j = 0; j < m; j++) {
console.log(matrix[j][0]);
}
Now we can simply loop over n columns:
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
console.log(matrix[j][i]);
}
}
The following is the visual representation of the above code snippets:
Note: swap i - j and m - n in row traversal to get column-wise traversal.
For the rest of the article, I am assuming that the reader has some prior knowledge of Breadth-First Search and Depth-First Search. I have attached some video tutorials on DFS and BFS in the resources🤌 section at the end as well.
Breadth-First Traversal
In Breadth-first traversal or Level-order traversal, we start by visiting all the neighboring nodes of our root node, after which we repeat the same process for the visited neighboring nodes until we have visited all the nodes.

Depending on the scenario, we can decide in what directions we can move in a matrix i.e. what adjacent nodes we can access from our current position. Here is how we generate indexes of adjacent nodes:
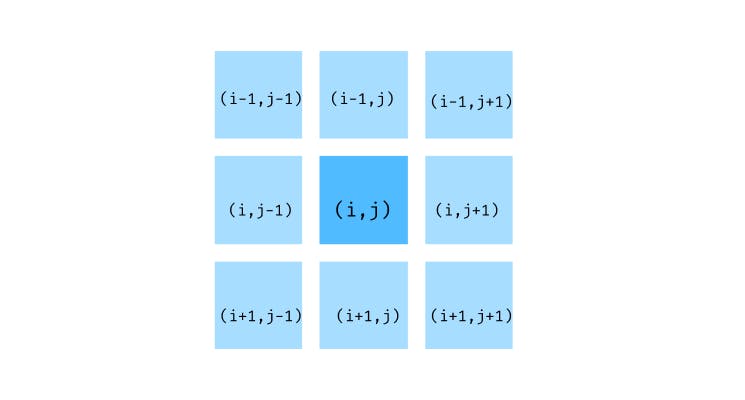
For this article, I will be considering only the top(i-1, j), right(i, j+1), bottom(i+1, j) and left(i, j-1) elements as neighbors. We will write a simple function to generate these nodes from a given node.
function generateEdges(x, y) {
const adjX = [-1, +1, 0, 0];
const adjY = [0, 0, -1, +1];
let edges = [];
for (let i in adjX) {
edges.push([x + adjX[i], y + adjY[i]]);
}
return edges;
}
We can now perform level-order traversal on the matrix:
function matrixTraversal(matrix, m, n) {
let queue = [];
queue.push([0, 0]);
let visited = matrix.map((row) => row.map((e) => 0));
visited[0][0] = matrix[0][0]; // considering (0, 0) as the root element
while (queue.length !== 0) {
let [x, y] = queue.shift();
console.log(matrix[x][y]);
let edges = generateEdges(x, y);
for (let edge of edges) {
let [i, j] = edge;
if (isValid(i, j, m, n, visited)) {
visited[i][j] = 1;
queue.push(edge);
}
}
}
}
// checks if node is valid and not visited
function isValid(i, j, m, n, visited) {
if (i >= 0 && i < m && j >= 0 && j < n && visited[i][j] === 0) {
return true;
}
return false;
}
function generateEdges(x, y) {
const adjX = [-1, +1, 0, 0];
const adjY = [0, 0, -1, +1];
let edges = [];
for (let i in adjX) {
edges.push([x + adjX[i], y + adjY[i]]);
}
return edges;
}
As you can see it is quite similar to breadth-first traversal of a tree, the only difference being the generateEdges() function.
Depth-First Traversal
While performing DFS on a tree, we travel to the deepest node and then backtrack to the parent node as soon as we find a node with no children. Similarly, in Depth-First Traversal of Matrix, we start by traveling to one of our neighboring elements and then repeating the process for the current element. We continue this process until we reach a dead-end, which in this case would be an element with all visited neighbors. Now just like in DFS for trees, we can backtrack to the last element where we have any unvisited neighbors. This process continues until all the elements in the matrix are visited. Here is a possible path for Depth-First Traversal:

The path of Depth-First Traversal is determined by the order of edges we generate. The path above was generated using the following edge generation function
function generateEdges(x, y) {
const adjX = [+1, -1, 0, 0];
const adjY = [0, 0, +1, -1];
let edges = [];
for (let i in adjX) {
edges.push([x + adjX[i], y + adjY[i]]);
}
return edges;
}
You can try finding new paths by changing the order of edges in the following code for Depth-First Traversal of a matrix:
function isValid(i, j, m, n, visited) {
if (i >= 0 && i < m && j >= 0 && j < n) {
if (visited[i][j] === 0) {
return true;
}
}
return false;
}
function generateEdges(x, y) {
const adjX = [0, +1, -1, 0];
const adjY = [-1, 0, 0, +1];
let edges = [];
for (let i in adjX) {
edges.push([x + adjX[i], y + adjY[i]]);
}
return edges;
}
function matrixTraversal(matrix, m, n) {
let stack = [];
stack.push([0, 0]);
let visited = matrix.map((row) => row.map((e) => 0));
visited[0][0] = matrix[0][0];
while (stack.length !== 0) {
let [x, y] = stack.pop();
console.log(matrix[x][y]);
let edges = generateEdges(x, y);
for (let edge of edges) {
let [i, j] = edge;
if (isValid(i, j, m, n, visited)) {
visited[i][j] = 1;
stack.push(edge);
}
}
}
}
The code is similar to Level Order Traversal the only difference being the use stack instead of a queue.
These were some of the ways you can traverse a matrix. I highly encourage you to check out some of their use cases as the author really stopped caring at this point. To make up for his carelessness, he added a bonus traversal method at the end.
Bonus: Spiral Traversal
Here is a visual representation of the path

You might have observed that in spiral order we are changing direction as soon as reach a vertex( i.e. the next element in that direction would be out of bound or would have already been visited ). And the order of direction change is simply right, down, left, top and repeat. The following code is easy to understand if you can wrap your head around the direction bit. Check out the code comments if you feel stuck.
function isNextValid(nextX, nextY, m, n, visited) {
// checks if the next element is within the
// bounds of given matrix
if (
nextX >= 0 &&
nextX < m &&
nextY >= 0 &&
nextY < n &&
visited[nextX][nextY] === 0
)
return true;
else return false;
}
function changeDirection(direction) {
// adds one to direction, resets to 0 if
// value goes beyond 4
return (direction + 1) % 4;
}
function matrixTraversal(matrix, m, n) {
// directions for spiral order
// right, down, left and up
let adjX = [0, 1, 0, -1];
let adjY = [1, 0, -1, 0];
// 0-> right, 1-> down, 2->left, 3-> up
let direction = 0;
let x = 0;
let y = 0;
let visited = matrix.map((row) => row.map((e) => 0));
visited[0][0] = matrix[0][0];
for (let i = 0; i < m * n; i++) {
visited[x][y] = 1;
console.log(matrix[x][y]);
// finding next element in the current direction
let nextX = x + adjX[direction];
let nextY = y + adjY[direction];
if (isNextValid(nextX, nextY, m, n, visited)) {
// jump to next element in the current direction
x = nextX;
y = nextY;
} else {
// change the direction and jump to next element
// in that direction
direction = changeDirection(direction);
x = x + adjX[direction];
y = y + adjY[direction];
}
}
}
Congrats! you made it to the end✨Hope you had as much fun reading as I had writing this post.